Reconstruction of the Field Consolidation Curve.
A soil in the field is assumed to have been consolidated to and then OMEGAmax rebounded to point A, and an embankment is assumed to be placed so that the effective stress will increase again. In calculating the settlement (Eq. 3.68), the strains must be calculated in terms of the height of the sample (or stratum
j in the field) at point A, not the original height, so the slopes of the reloading are virgin curves that must be suitably corrected. Similar corrections are required if a soil sample is to be used as representative of a stratum, but does not come from the center of the stratum, and for various other applications.
The occasional inconveniences due to changed total heights are minor, and some engineers use the types of graphs shown in Figure 3.19, but most geotechnical engineers prefer to avoid confusion by calculating strains in terms of a constant height. The height selected is the height of solids Hs, a fictitious height defined as
where Vs is the volume of solid mineral grains and A is the cross-sectional area of the test specimen. The vertical strains are calculated in terms of Hs and are
because AVs 0. Thus, void ratios are plotted instead of strains, and the change in void ratio is a strain expressed in terms of the constant height of solids. The settlement equation (Eq. 3.68) becomes
Thus
The e-log OMEGA curve for an overconsolidated clay may have the appearance of the curve shown in Figure 3.22. If a structure is placed on the soil deposit so that OMEGA O increases to OMEHA F the settlement is then
Figure 3.22 Consolidation curve for overconsolidated clay.
The settlement S that results from increasing the loading from omega1 to omega2 is computed by combining Eqs. 3.74 and 3.75 using
In the usual notation, the initial condition of the normally consolidated soil is denoted by the subscript 0 and the final condition by the subscript ƒ. The settlement for layer j is then

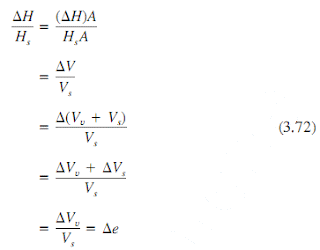






0 comments:
Post a Comment